


This website has been superceded.
Go to the new Shoalhaven Bushwalkers website by clicking the link below
www.shoalhavenbushwalkers.com(Scroll down to see the old page)






(Scroll down to see the old page)



 |
|
|
|
The new series of topographic maps use a different datum to the old series, with the grid references on the map moving about 200 metres in a north easterly direction. This means that all of the grid references mentioned in our walk reports and track notes will be soon out of date. I wondered if there was a simple way to make conversion from the old grid references to the new grid references by the addition (or subtraction) of a set figure ie. old GR645372 minus 1001 = new GR644371.
Finding nothing specific on the Internet, I went in search of information which would allow me to calculate the figure myself. Here is what I found ...
Apparently, the old topographic maps were based on the Australian Geodetic Datum (AGD). This has now been replaced by the Geocentric Datum of Australia (GDA), which is part of a global coordinate reference frame and is directly compatible with the Global Positioning System (GPS). The following is a quote from the Geocentric Datum of Australia Technical Manual Version 2.2 put out by the Intergovernmental Committee on Surveying and Mapping.
"ITRF92, on which GDA is based, was realised using Very Long Baseline Interferometry, and GPS and Satellite Laser Ranging observations at 287 globally distributed stations. However, the coordinates for Johnston, the origin station for the Australian Geodetic Datum (AGD), were based on a selection of 275 astro-geodetic stations distributed over most of Australia."
(Incidentally, Johnston is about 250kms SSW of Alice Springs, about 30km from the small town of Kulgera, which is the first town on the Stuart Highway north of the South Australian border. I now resume the quote.)

Johnston Geodetic Station
"The adoption of this origin and the best fitting local ellipsoid, the Australian National Spheroid (ANS), meant that the centre of the ANS did not coincide with the centre of mass of the earth, but lay about 200 metres from it. Hence, the GDA94 coordinates of a point appear to be about 200 metres north east of the AGD coordinates of the same point. The precise size and orientation of the difference will vary from place to place."
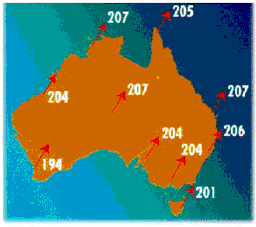
Map showing differences in displacement
As you can see from this map of Australia, the difference in distance varies by up to 13 metres - from 194 metres in Perth, to 207 metres in Alice Springs, Darwin and Brisbane. Sydney's variation is 206. This will not make any great difference to us, as our usual six figure grid references are only accurate to within 100 metres anyway.
I could find no data on the precise direction of the difference - 200 metres to the north-east seems to be as good as we will get. I could not even find out whether it was magnetic north-east or grid north-east or true north-east. So, for the purposes of this exercise, I will assume that the distance is 200 metres, and that the direction is grid north-east.
Now, as we all know, the coordinate system on our topographic maps is based on the Universal Transverse Mercator grid, commonly known as UTM. I gave a presentation on UTM a couple of years ago when the club purchased its GPS, so I am sure that you are all up to speed on it.
One of the best features of UTM is that the numbers used in the grid references actually have meaning - they are in fact distances. On a GPS coordinate display, you will see two figures. The six digit one is the easting, and the seven figure one is the northing. If each of these figures increases by just one, the location of the new point is one metre further east and one metre further north of the original position.
The six figure grid references we use on maps are actually three figures for the easting, and three figures for the northing. They still represent distances, but now the unit is 100 metres. If each of these figures increases by just one, the location of the new point is 100 metres further east and one hundred metres further north. (Technically, it is actually somewhere within a 100 metre square area which is 100 metres further east and one hundred metres further north, but we don't have to worry about that now).
To work out the change in metres to the east, and metres to the north brought about by a shift 200 metres to the north east we can use the Pythagorean Theorem of a2 + b2 = c2, or for our purposes, the easting squared plus the northing squared = 200 metres squared. Once we have done the arithmetic, we find that the easting and northing are 100 times the square root of 2 metres, or about 141.42 metres.
This is about one and a half of our 100 metre squares, and it means that sometimes the new easting and northing will differ from the old one by either 1 or 2, depending on precisely where within the 100m square the point is actually located. See the diagram below -
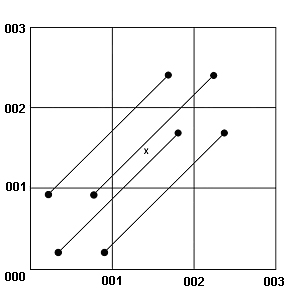
Each square is 100 metres
Looking at the above figure, and remembering that it is the grid which has moved 200 metres to the north-east, the point shown as "x", which would have been GR001001 on the old maps, now becomes GR000000 on the new maps. So, to convert an old grid reference to a new grid reference we have to subtract one of four figures, depending on the precise location of the point in question - either 1001, 1002, 2001 or 2002. To convert a new grid reference to an old grid reference, we have to add one of those four numbers.
Because of this lack of precision, and also because more problems appear at the boundaries of the six degree strips in the UTM system, it is recommended that we simply refer to grid references by their datum ie. either AGD vs GDA, or simply by saying the old datum or the new datum, respectively.
(September 2006)
TOP